About Trees, different Traversals and BST
A tree is a data structure made up of nodes or vertices and edges without having any cycle. The tree with no nodes is called the null or empty tree. A tree that is not empty consists of a root node and potentially many levels of additional nodes that form a hierarchy.
Root: The top node in a tree.
Child: A node directly connected to another node when moving away from the Root.
Parent: The converse notion of a child.
Siblings: A group of nodes with the same parent.
Descendant: A node reachable by repeated proceeding from parent to child.
Ancestor: A node reachable by repeated proceeding from child to parent.
Leaf: A node with no children.
Internal node: A node with at least one child.
Degree: The number of sub trees of a node.
Edge: The connection between one node and another.
Path: A sequence of nodes and edges connecting a node with a descendant.
Level: The level of a node is defined by 1 + (the number of connections between the node and the root).
Height of node: The height of a node is the number of edges on the longest path between that node and a leaf.
Height of tree: The height of a tree is the height of its root node.
Depth: The depth of a node is the number of edges from the tree's root node to the node.
Forest: A forest is a set of n ≥ 0 disjoint trees.
 |
| Tree |
Tree Terminology
Lets see some tree terminologies:-Root: The top node in a tree.
Child: A node directly connected to another node when moving away from the Root.
Parent: The converse notion of a child.
Siblings: A group of nodes with the same parent.
Descendant: A node reachable by repeated proceeding from parent to child.
Ancestor: A node reachable by repeated proceeding from child to parent.
Leaf: A node with no children.
Internal node: A node with at least one child.
Degree: The number of sub trees of a node.
Edge: The connection between one node and another.
Path: A sequence of nodes and edges connecting a node with a descendant.
Level: The level of a node is defined by 1 + (the number of connections between the node and the root).
Height of node: The height of a node is the number of edges on the longest path between that node and a leaf.
Height of tree: The height of a tree is the height of its root node.
Depth: The depth of a node is the number of edges from the tree's root node to the node.
Forest: A forest is a set of n ≥ 0 disjoint trees.
Tree Node
Tree Node has a data part and references to its left and right child nodes.
In a tree, all nodes share common construct.
Tree Traversals
Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree. Unlike linear data structures (Array, Linked List, Queues, Stacks, etc) which have only one logical way to traverse them, trees can be traversed in different ways. Following are the generally used ways for traversing trees.
- In-order Traversal
- Pre-order Traversal
- Post-order Traversal
In-Order Traversal
In this traversal method we first visit the left sub-tree, then the root and later the right sub-tree. If a binary tree is traversed in-order, the output will produce sorted key values in an ascending order.
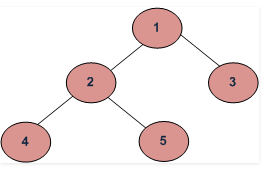
For e.g.
Output of the In-Order traversal for above tree is
4 -> 2 -> 5 -> 1 -> 3
Algorithm Inorder(tree)
1. Recursively traverse the left subtree, i.e., call Inorder(left-subtree)
2. Visit the root
3. Recursively traverse the right subtree, i.e., call Inorder(right-subtree)
Pre-Order Traversal
In this traversal method we first visit the root node, then the left sub tree and finally the right sub-tree.
For e.g.
Output of the In-Order traversal for above tree is
1-> 2 -> 4 -> 5 -> 3
Algorithm Preorder(tree)
1. Visit the root.
2. Recursively traverse the left subtree, i.e., call Preorder(left-subtree)
3. Recursively traverse the right subtree, i.e., call Preorder(right-subtree)
Post-Order Traversal
In this traversal method we first visit the left sub tree, then the right sub-tree and finally the root node.
For e.g.
Output of the In-Order traversal for above tree is
4-> 5 -> 2 -> 3 -> 1
Algorithm Postorder(tree)
1. Recursively traverse the left subtree, i.e., call Postorder(left-subtree)
2. Recursively traverse the right subtree, i.e., call Postorder(right-subtree)
3. Visit the root
Binary Search Tree(BST)
In binary tree, every node can have maximum two children but there is no order of nodes based on their values. Binary search tree is a type of binary tree in which all the nodes in left subtree of any node contains smaller values and all the nodes in right sub-tree of that contains larger values as shown in following figure
Operations on a Binary Search Tree
Following Oprations performed on BST
1. Search
2. Insertion
3. Deletion
Search Operation
Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.
Algorithm
node* search(int data){
struct node *current = root;
printf("Visiting elements: ");
while(current->data != data){
if(current != NULL) {
printf("%d ",current->data);
//go to left tree
if(current->data > data){
current = current->leftChild;
}//else go to right tree
else {
current = current->rightChild;
}
//not found
if(current == NULL){
return NULL;
}
}
}
return current;
}
Insert Operation
Whenever an element is to be inserted, first locate its proper location. Start searching from the root node, then if the data is less than the key value, search for the empty location in the left subtree and insert the data. Otherwise, search for the empty location in the right subtree and insert the data.
Algorithm
Node * Insert(Node * root, int data)
{
if(root == nullptr)
{
Node * NN = new Node();
root = NN;
root->data = data;
root->left = root ->right = NULL;
}
else
{
if(data < root->data)
{
root->left = Insert(root->left, data);
}
else
{
root->right = Insert(root->right, data);
}
}
return root;
}
Deletion Operation in BST
In a binary search tree, the deletion operation is performed with O(log n) time complexity. Deleting a node from Binary search tree has following three cases:-
Case 1: Deleting a Leaf node (A node with no children)
Step 1: Find the node to be deleted using search operation
Step 2: Delete the node using free function (If it is a leaf) and terminate the function.
Case 2: Deleting a node with one child
Step 1: Find the node to be deleted using search operation
Step 2: If it has only one child, then create a link between its parent and child nodes.
Step 3: Delete the node using free function and terminate the function.
Case 3: Deleting a node with two children
Step 1: Find the node to be deleted using search operation
Step 2: If it has two children, then find the largest node in its left subtree (OR) the smallest node in its right subtree.
Step 3: Swap both deleting node and node which found in above step.
Step 4: Then, check whether deleting node came to case 1 or case 2 else goto steps 2
Step 5: If it comes to case 1, then delete using case 1 logic.
Step 6: If it comes to case 2, then delete using case 2 logic.
Step 7: Repeat the same process until node is deleted from the tree.





Comments
Post a Comment